マイクロマウスのアルゴリズムについて③

佐倉です。日曜日なのでマイクロマウスのアルゴリズムの話を書いていきます。

今回は、足立法の詳細を書いていきます。
前回のおさらいです。足立法の流れは、こんな感じになるのでした。

ゴールへの最短経路に沿って１マス進む
壁を読み取る
最短経路を導き直す

をゴールに着くまで繰り返す。

壁を読み取る事ができる、できないについては、探索アルゴリズムの知る所ではないので、置いておいて
現在知っている壁の情報を元に、ゴールまでの最短経路を導く事が重要なようです。

どうするのが良いでしょうか？
マイクロマウスでよく使われるのは、歩数マップという考え方です。
どう使えるかは放っておいて、どんなものかを説明します。
下の図のような、数字が書き込まれたマップです。

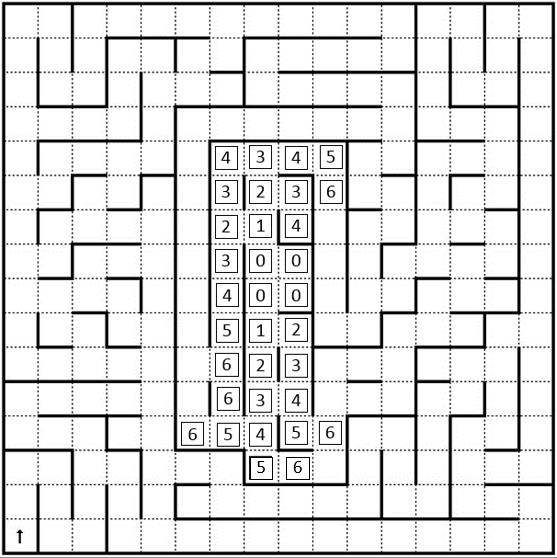
歩数マップの作り方は、
最初に、ゴールに０を書き、数字が書かれたマスに隣接した空白のマスに、マスの数字+1を書き込んで行く。
という感じです。ただし、空白のマスに数字を書く時に、今書いている数字より小さい数字を書ける場所がないかどうか確認します。
たとえば、上で例に出した迷路で、ゴールの０から上に向かって一気に、0123・・・と書いていくのではなく、
ゴールの０に隣接した空白は上と下に２つあるので、１を２つ書き込み、1に隣接する空白は4箇所あるので２を4箇所・・・というように書いていきます。

このマップを初めて見る方は、画像を印刷するか、ペイントか何かで、手を動かして歩数マップを完成させてみてください。

完成したマップで何ができるかというと、ゴールまでの最短歩数を調べることができます。
１マス移動する事を1歩と見立て、ゴールまでの歩数がマップ状に書き込まれているので、歩数マップというわけです。

最短歩数がわかると、何ができるのでしょう？
ゴールまでの歩数が小さければ、よりゴールに近いということになります。
つまり、自分のマスに隣接したマスの中で、自分より小さい数字が書かれたマスの方に行けば、必ずゴールに近づくことができます。
しかも、最短歩数を辿っていっているので、無駄な経路は選びません。つまり、
歩数マップを作り、小さい数字が書かれた方向へマスを辿って行く経路は、ゴールまでの最短歩数を辿る経路になる。
と言えます。

歩数マップを作ってみた方は是非、適当に選んだマスから数字の小さい方へ辿ってみてください。
機械的に最短歩数経路が求まるはずです。

足立法の最短経路を導くという部分がこれで終わりました。意外と簡単ですよね。
最短走行をする時の最短経路の導出も歩数マップを使って行う事ができます。

次回は、足立法を拡張して全面探査をする方法を紹介します。