佐倉です。DCマウス入門の連載の続きです。
今回はいよいよDCマウスの制御(の一例)を解説していきます。
制御の種類
第二回でモータのトルクと運動の関係、
第三回でモータのトルクと出力するDuty比の関係を解説しました。
これらに従って、させたい運動(加速度と角加速度)を決め、計算したDuty比を出力すれば、だいたいその通りの運動をします。
このように、指令値を出力しっぱなしの制御をオープンループ制御や、フィードフォワード制御などと呼びます。
ステッピングモータのように、指令と実際の動きの差が非常に小さいシステムの場合、これだけでうまく行きます。
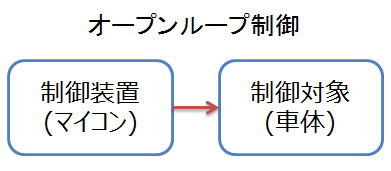
しかしDCマウスの場合、そうは行きません。
フィードフォワード制御をした上で生じた誤差を修正するために、フィードバック制御を行う必要があります。
このように、フィードフォワードとフィードバックを同時に行う制御を二自由度制御と呼びます。
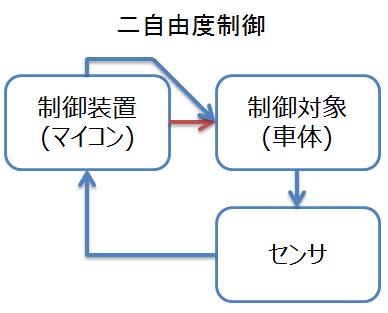
DCマウスを始めたてで、フィードフォワードは難しいからフィードバックだけで動かそうとしている人をよく見かけますが、
フィードバックだけで動かすのは大変なので(指令通り動かすのは原理上不可能)、最初から2自由度制御系を作るのをオススメします。
何を制御するか
さて、ここまで何も考えずに制御、制御、と言ってきましたが何を制御するのでしょう?
マイクロマウスでしたい制御は、設計した経路を辿る制御です。
経路を辿るという制御を正確に作ろうとすると車体の位置を正確に把握する必要がありますが、これは非常に難しいです。
そこで、マイクロマウスでよく行われているのは、経路を速度と角速度で設計して(指令値)、それを制御によって綺麗に辿るという方法です。
経路を速度と角速度で設計という所を軽く補足しておきます。
速度v(t)[m/s]、角速度ω(t)[rad/s]で運動している時、微小時間Δt[s]で区切って考えると、円弧軌跡の弧の長さL(t)[m]さ半径r(t)[m]がそれぞれ、
L = v × Δt
r = v / ω
となるので、十分小さなΔtを用意して、辿りたい経路を円弧区間の連続と考えれば、vとωで経路を設計できます。
フィードバック制御
速度と角速度を制御してやれば実績のある制御ができる事がわかりました。
フィードフォワード制御はほとんど解説が済んでいるので、フィードバック制御を解説して行きます。
フィードバック制御には、よく知られているPID制御を使います。PID制御についてはいくらでも資料があるので、調べてください。
式は教科書通りです。速度も角速度も同じです。
out = P×en + I×?(e×Δt)n + D×(en-en-1)/Δt
(調整のための傾向として、D成分は速度、角速度共にあまり有効ではありません。)
制御の合成
フィードバックの出力が求まったので、二自由度の制御にしましょう。足すだけです。
速度のフィードフォワード出力をFFS[m/s2] (妙な表現ですが、出力したい加速度です。)
角速度のフィードフォワード出力をFFA[rad/s2] (妙な表現ですが、出力したい角加速度です。)
速度のフィードバック出力をFBS[m/s2]
角速度のフィードバック出力をFBA[rad/s2]
とすると、車体が出力するべき加速度a[m/s2]、角加速度α[rad/s2]は
a = FFS + FBS
α = FFA + FBA
となります。
あとは、第二回と第三回の式を使って、Duty比に変換して出力してあげると、めでたく制御がかかったマウスが出来上がります。
センシング
ここまででは、PID制御のerrorを計算するためのセンシングの部分が抜けています。ここも解説していきます。
まず、速度ですが、今回は重心での速度ということでモデル化しているのでした。
車軸が重心を通っていると考えているので、重心の速度vは左右のタイヤでの速度vR、vL(エンコーダから計算)から
v = (vR + vL) / 2
と計算できます。
次に角速度系です。
まずは、積んでみたものの使い方がわからないという声がちょくちょく聞こえてくる、ジャイロが積んである場合です。
上で解説した制御系を作っていれば、角速度のPID制御のerrorを計算する時に、
error = 目標角速度[rad/s] – ジャイロから計測した角速度[rad/s]
とするだけです。簡単ですね。
気をつけるのは、
ジャイロの感度はパラメータとして調整(超重要)
ジャイロのリファレンス点は走り出しの前に取得(数百回?数千回値を取って、平均を出す)
の2点だけです。
ちなみに、ジャイロのリファレンス点などを整数型でどうにかしようとしている例を見かけますが、積分するような用途でそれは厳しいです。
50MHz動作のSH2-tinyや、72MHz動作のCortex-M3などであれば、浮動小数点で制御計算をまわして1ms周期で十二分に計算が間に合うのは実証済みなので素直に全部浮動小数点型にしてしまいましょう。
次に、ジャイロが無い場合です。この場合、正確な角速度は測れません。
ジャイロが無いのは(この考え方で動かす場合)機能に欠陥があると云う事になります。
一応、精度は出ませんが近似的に角速度を出す方法があります。
角速度 = vR – vL / トレッド幅
と計算する方法です。
探索くらいの速度ではそれなりに動きますが、速く走らせようとすると、角度がうまく合わなくなってくると思います。
ジャイロは難しい物じゃないので、積極的に使って行きましょう。
今回はここまでです。
次回は、壁を見てまっすぐ走る方法の一例を紹介します。
 迷路 |
 柱 柱 |
 壁 壁 |


