DCモータを使ったマイクロマウス入門②

佐倉です。
前回おおまかに流れを説明した、DCマウス入門講座を進めていこうと思います。
今回は車体の運動についてです。

今回はマイクロマウスの車体の運動です。
まず、DCモータを使ってマウスを動かす時に、ステッピングモータに比べて何が面倒かというと、指定した速度で動かすのが難しいという事です。
もっと大雑把に言ってしまうと「入力と出力の関係がわかりづらい」ということですね。

というわけで、今回の車体の運動と、次回のモータの動かし方と特性については、入力と出力の関係を説明していく事になります。

今回の目的として、マイクロマウスの運動を式で表現したいわけですが、どのような表現方法があるでしょうか。
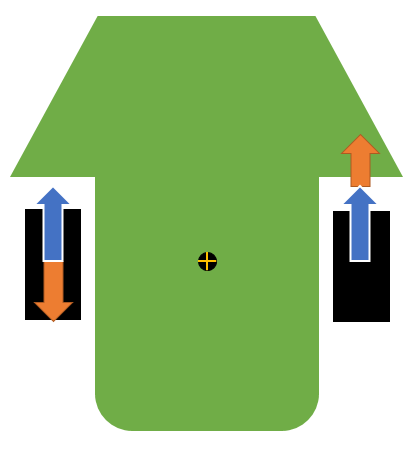
まず、物理的に考えた時、マイクロマウスとは何ぞやという所を考えると、2次元平面上の剛体として捉えて問題ないでしょう。
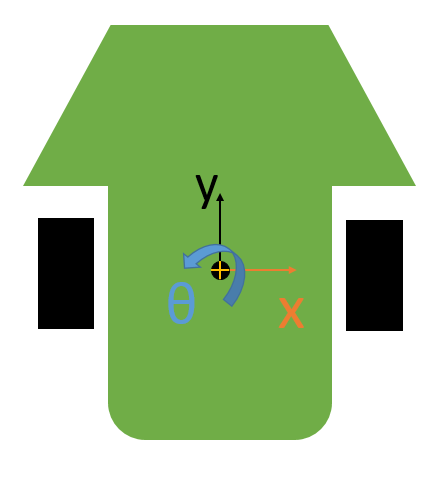
2次元平面上の運動は、通常直交座標のxとyで表すことができますが、剛体なので角度も必要になります。
x,y,θの3つと、その速度、加速度で運動を記述できそうです。

さて、ここまでで、マイクロマウスを剛体として捉えていたのですが、マイクロマウスの特徴を使って、１つ変数を削る事ができます。
マイクロマウスのほとんどは差動二輪型のロボットですね。その場合にマイクロマウスに固定された座標系(ローカル座標系)で考えると、車体進行方向に向かって直交する方向へは運動しません。(滑る領域まで速くなった時には考える必要が出てきます。)
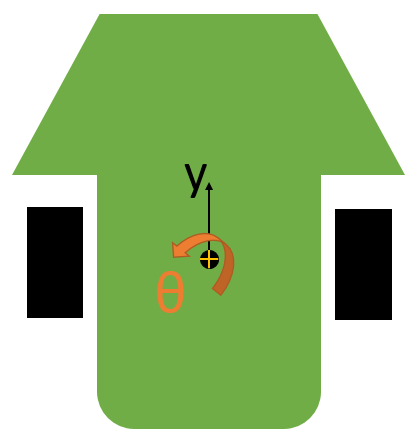
y,θとその速度、加速度で運動を記述できそうです。今回はこのローカル座標系で考えて行きます。

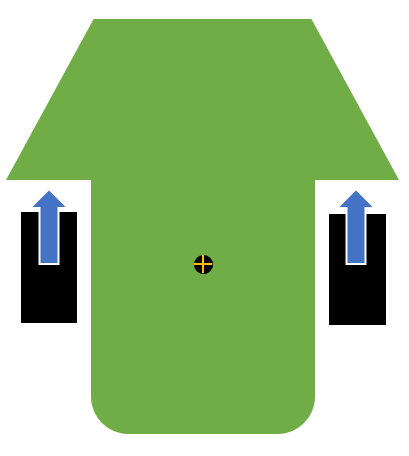
さて、この距離と角度について、どのように運動を考えていくかというと、運動方程式を使います。まずは距離(並進運動)について考えましょう。
並進運動の運動方程式はF=maです。F[N]という力が与えられた時、質量m[kg]の物体は加速度a[m/s^2]で運動しますという法則ですね。軸一本で考えているので、スカラーです。

こういう風に運動させたい→どう出力したら良いのか　を考えているので、運動＝加速度aを自分で決めます。すると、重量mは決まっているので、そのまま運動方程式を使って、F=maで車体に加える力が求まります。
タイヤは通常2個ついているので、タイヤが車体に伝えなければならない力の大きさF’は、
F’=F/2=ma/2
となります。

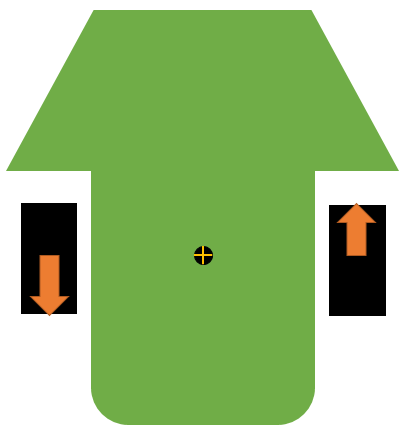
角運動についての運動方程式は、N=Iαです。文字はそれぞれ、

N　トルク[N・m]
I　慣性モーメント[kg・m^2]
α　角加速度[rad/s^2]

の意味があります。F=maとそのまま対比して、N：力のようなもの、I：質量のようなもの、α：加速度のようなもの
と捉えて問題ありません。
ここでも、αは自分で決める運動に関する値、Iは車体固有の値なので、N=Iαで車体を回転させるのに必要な重心まわりのトルクが計算できます。

タイヤがどれくらいの力を出せばNのトルクを出せるかについて考えていきます。
ここで１つ、重心は車軸上の真ん中にあると簡略化して考えます。
(慣性モーメントは重心まわりが一番小さくなるので、このように設計するのが良いと思います。)
剛体に腕の長さL[m]、大きさF_ω[N]の偶力が働く時、N=F_ωLで偶力が計算できるのでした。
上の、回転についての運動方程式と連立して
Iα=_FωL
F_ωについて解いて
F_ω=Iα/L
となります。Lは偶力の腕の長さ＝タイヤ間の距離＝トレッド幅です。

さて、これで並進運動と角運動の式がそれぞれ出ました。この２つは直交しているので、単純に足し合わせる事ができます。
加速度a、角加速度αで運動させたい時にタイヤが伝えるべき力は、反時計回りに角度の正方向を取ると、
右タイヤが出力する力F_R=F’+F_ω
左タイヤが出力する力F_L=F’-F_ω
となります。

ここで、タイヤが力を出力するとはどういう事だ、となると思います。
タイヤは回転する物なので、トルクを出力できるのは理解できると思います。
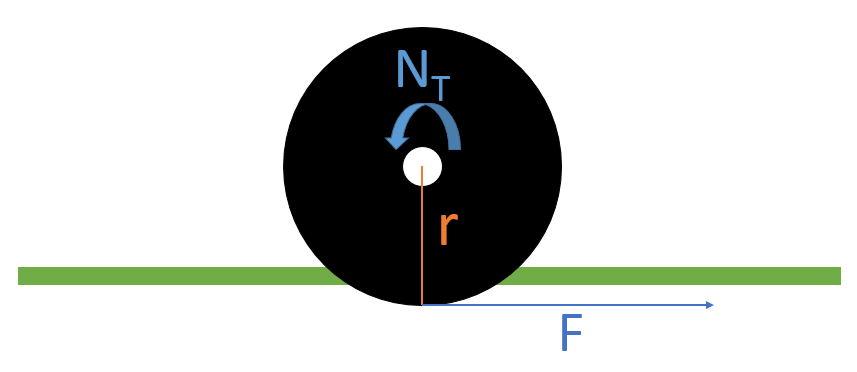
それが地面に接し、滑らずに力を伝えた場合、タイヤの半径をうでの長さと見て、トルクを力として伝える事になり、車体はその反作用を受けることになります。
具体的には、伝える力(の反作用)をF[N]、車軸まわりのトルクをN_T[N・m]タイヤの半径をr[m]とすると、N_T=F・rですね

さて、何がタイヤにトルクを伝えているかというと、ギヤを通し、DCモータが力を伝えています。
ギヤは、テコの原理を使って、長い距離移動しなければならなくなる代わりに、大きな力を取り出すことのできる部品です。
2：1のギヤを組んだ場合、モータは2倍の距離回転しなければなりませんが、ギヤの軸まわりでは、モータの軸まわりのトルクが2倍になって出力されます。
つまり、ギヤ比n：1の車体を作成した場合、車軸まわりのトルクは、モータの軸まわりでは1/nになる＝負荷が軽減されるということです。

組み合わせると、加速度a、角加速度αで運動させたい時にモータの軸まわりで出力しなければならないトルクN_R、N_Lは、
N_R=F_R・r/n
N_L=F_L・r/n
となります。ギヤ比を上げるとモータの負荷が軽減され、タイヤ径を増すと、モータの負荷が上がるというような事情が読み取れると思います。

次回は、モータから望みのトルクを出力する方法を紹介します。